Magyarul

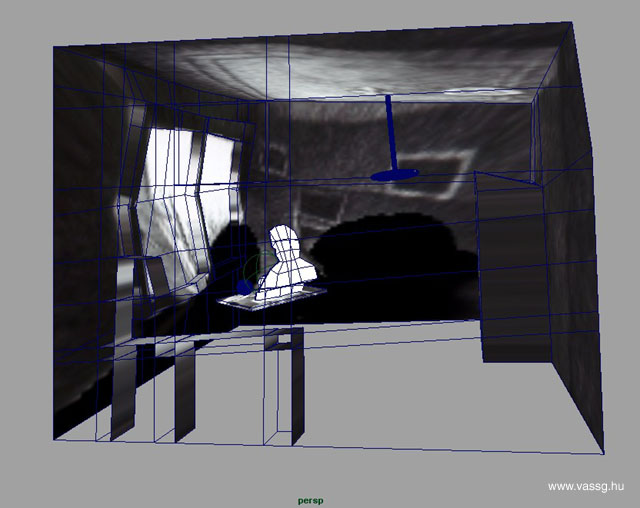
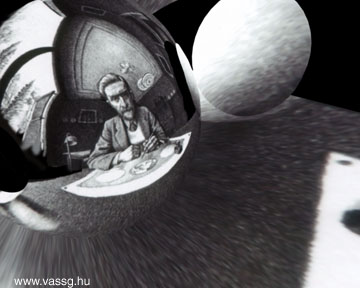
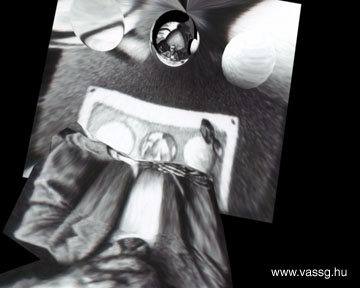
I was a great fan of M. C. Escher's work since I was a little kid. In the drawing classes in elementary school I tried to copy Vasarely's and Escher's paintings and drawings and figure out the idea behind them. These images were not just pieces of art for me rather some sort of geometrical or mathematical riddles. This is not surprising since Escher considered himself more like a mathematician than an ordinary graphic artist. (However, he had no mathematical qualification.)

A while ago I happened to take a look in one of the albums of Escher and found some interesting pictures of reflecting spheres (or mirror balls). These caught my attention because the images of mirror balls are used extensively in computer graphics to reconstruct reflections. It is possible in almost any 3D package to "backproject" the mirror ball image to any surface, thus rebuilding the original environment. So I decided to rebuild the artist's room based on the lithograph called Three Spheres II (1946).

I started with a polygon cube representing the room. It is visible on the picture that the artist has sat at a table in the corner, so I placed a poly plane and a "virtual Escher" in the corner. The center of the projection was the point where the original sphere was supposed to be (I used Maya - ball projection). I played around a while to match the exact orientation of the image, the goal was to project the edges on the image to the edges of the polygon cube. Unfortunately the use of mirror ball images is not that easy since there is always some distortion which should be compensated (my solution for the problem).

Another issue was the occluded portion of the room. Both Escher, the table and the balls hide a great part of the room so I tried to paint the hidden walls by hand in Photoshop. There were two versions of the picture with the reflecting sphere: the original with the artist and the painted without the artist (you don't want to see Escher projected on the wall). Finally I refined the polygon cube to have a nicer match with the projection and to model some of the furniture.

The modeling and matching of the texture projection was done in one day. After that I made a 1200 frame long fly-through animation to show the whole room from different angles. It is interesting that the reflecting of the final drawing is visible in the sphere so it is also visible on the table. It is blurred a lot but still recognizable. The first and the final images of the animation show the reflection of the sphere in the virtual room, which is exactly the same as the original reflection.

I have found another interesting experiment based on Escher' work here: escherdroste.math.leidenuniv.nl

Interesting experiment using Lego pieces to reconstruct one Escher image www.lipsons.pwp.blueyonder.co.uk/escher/ascending.html