English

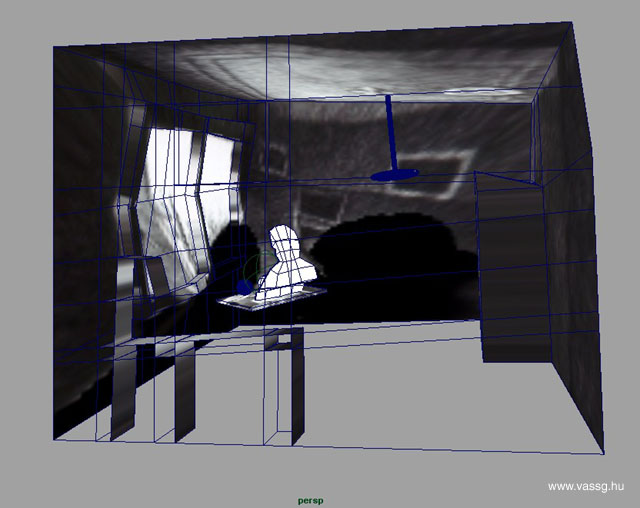
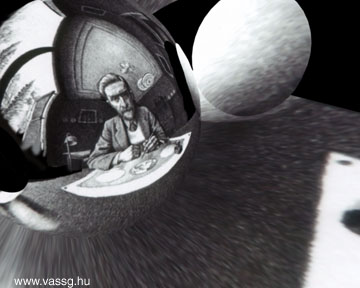
Már egészen kiskorom óta nagy rajongója vagyok M.C. Escher munkáinak, az általános iskolai rajzórákon számtalanszor próbáltam Escher és Vasarely képei leutánozni. Escher művei számomra - a "hagyományos" művészeti alkotásokkal szemben - nem elvont gondolatokat vagy érzéseket, hanem érdekes, már-már matematikai összefüggéseket tolmácsoltak. Ez nem is volt véletlen, hiszen maga Escher is írja: "E művek [az album képei] alapjául szolgáló eszmék nagyobbrészt arról a csodálatról és csodálkozásról tanúskodnak, amely engem a környező világ törvényszerűségei iránt elfog. [...] Jóllehet semmiféle egzakt tudományos képzettségem nincs, mégis közelebb érzem magam a matematikusokhoz, mint tulajdonképpeni pályatársaimhoz."

Nemrég ismét a kezembe került Escher "Grafikák és rajzok" című albuma (Taschen 1992). A Tükröződések című fejezetben rábukkantam több rajzára, melyen tükröző gömb látható. Ez azért keltette fel ismét az érdeklődésemet, mert a 3D grafikai programok a tükörgömbös fotók alapján képesek a környezet képét visszaállítani, azaz a képet "visszavetíteni" tetszőleges 3D felületre. Elhatároztam hát, hogy megépítem a Három golyó II. (Drie Bollen II) című litográfia alapján a tükrözodésben látható szoba egyszerűsített, virtuális mását.

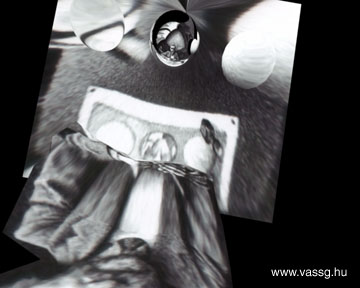
A munkát egy négyzet alapú téglatest létrehozásával kezdtem. Mivel a képen látszik, hogy a rajz a szoba sarkában készült, így a sarokba helyeztem az asztalt és a mellette ülő művészt reprezentáló polygon felületet. A felületekre rávetítettem a rajzot a Maya "ball projection" eszközével. A vetítés középpontjának a szoba azon pontját adtam meg, ahol a tükröző golyó lehetett. A vetítés pontos irányát és helyét megpróbáltam a lehető legjobban eltalálni, a kép torzulását azonban teljesen nem lehetett kikorrigálni. A "ball projection" modellje ugyanis azt feltételezi, hogy a rajzoló végtelen nagy távolságra volt a gömbtől, így a tér teljes képe látszik a tükröződésben. Ez persze sosem teljesül. (A probléma megoldása itt)

Mivel a rajzoló Escher a szoba jelentős részét eltakarja, csináltam egy olyan verziót is, ahol megpróbáltam kézzel kiretusálni a művészt. Később ezt a képet vetítettem a falakra, így nem zavarja a látványt a "falra kent" Escher. (A csillárt például nem javítottam ki, így az a plafonon is megjelenik...) A bútorokat, az asztalt és a rajzolót helyettesítő felületeket próbáltam úgy formázni, hogy a lehető legjobban illeszkedjen rájuk a textúra.

A modell építése és a textúrázás egy hosszú délután alatt elkészült, ezután már csak a kamera mozgását kellett létrehozni. Az 1200 kocka hosszú animáció során törekedtem arra, hogy a néző az egész szobát láthassa, körbejárja. A kamera a művész elött fekvő képre is ráközelít, így láthatjuk, hogy az eredeti rajzon tényleg a végső mű tükröződése látható. Az animáció a virtuális tükörgömb képével indul és fejeződik be, hiszen ez a kép szolgált a "kísérlet" alapjául.

Escher egy másik képével kapcsolatban szintén találtam érdekes kísérleteket: escherdroste.math.leidenuniv.nl

Amikor a Lego játék és Escher egy képe találkozik: www.lipsons.pwp.blueyonder.co.uk/escher/ascending.html